


Next: The general case: multiple
Up: . Introduction: Variable gain image
Previous: Estimation with more than
Generally the relative exposure values  are not known a-priori.
Thus simultaneously solving for
are not known a-priori.
Thus simultaneously solving for 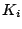 and
and 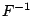 is an optimization
problem:
is an optimization
problem:
- Initially, pairwise comparagrams are constructed and unrolled, each
assuming an arbitrary value of
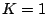 (e.g.
(e.g. 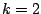 ).
The resulting
).
The resulting 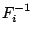 function estimates for each pair of images
will have the same overall shape, but each be scaled differently,
apart from noise.
function estimates for each pair of images
will have the same overall shape, but each be scaled differently,
apart from noise.
- Next these estimates of
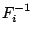 are used to estimate
the relative
are used to estimate
the relative 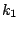 values. Without loss of generality,
values. Without loss of generality,
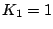 may be assumed, and
may be assumed, and
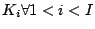 may be found.
may be found.
- Next the estimates of
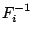 are consolidated (averaged together)
by using the above estimates of
are consolidated (averaged together)
by using the above estimates of
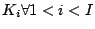 to register
them. This registered and averaged
to register
them. This registered and averaged  is now used to
re-estimate the
is now used to
re-estimate the 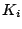 values, by comparing ratios:
K_i = F^-1 - Q
where
values, by comparing ratios:
K_i = F^-1 - Q
where 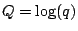 is the logarithm of the reference quantity of light.
(At this point, this first guess is often good enough to stop, but
may undergo successive refinements by continuing as follows...)
is the logarithm of the reference quantity of light.
(At this point, this first guess is often good enough to stop, but
may undergo successive refinements by continuing as follows...)
- Finally, if desired, images are sorted in increasing order
of exposure (least to greatest), and a final estimate
of
 is made across all pairs of images,
using the estimates of
is made across all pairs of images,
using the estimates of 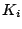 .
.
- If desired, this process may again be repeated, e.g. using that estimate
 to again estimate
to again estimate 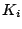 and so on.
and so on.
Subsections



Next: The general case: multiple
Up: . Introduction: Variable gain image
Previous: Estimation with more than
Steve Mann
2002-05-25